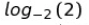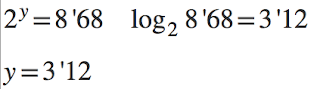Prueba 5

1)

Logaritmo = exponente

Más extensamente dicho, un logaritmo es el exponente al que hay que elevar un número (base), para obtener otro número determinado.

2)

Propiedades de los logaritmos:

- No existe ni el logaritmo de 0, ni el logaritmo de bases negativas.

- Definición de logaritmo, que es:

- El logaritmo de 1 es 0.

- El logaritmo de un producto es igual a la suma de los logaritmos de los factores:

- El logaritmo de un cociente es igual a la resta del logaritmo del dividendo menos el del divisor:

- El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base:

- El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz:

- Para el cambio de base en calculadoras antiguas: (donde c es 10 o e)

3)

La escala logarítmica es una escala de medida, que se utiliza para representar más cómodamente cantidades físicas en forma de porcentajes ( y no en valor absoluto, como en la escala lineal).

El gráfico logarítmico busca mantener constantes las proporciones, no los números brutos.

Diferenciamos a ésta escala de la lineal, ya que no muestra bien la evolución de lo que sea que estemos hablando, cuando esto abarca un rango amplio. En esas situaciones especiales, hay que pasarse al logarítmico. En este ejemplo se ven las diferencias:

4)

Para que el resultado sea dos, hay que elevar 1/2 a -1, ya que al haber una potencia negativa, para convertirla en positiva debemos pasar el divisor al dividendo y el dividendo al divisor, por lo que nos queda 2 elevado a 1.

Para que el resultado sea 1/2, hay que elevar 2 a -1 también, por la misma razón.
  

Para que el resultado sea -2, hay que elevar 1/2 a 1, ya que si pasa el dos del divisor     al dividendo, se vuelve negativo, y por tanto -2 elevado a 1, es igual -2.

No existe el logaritmo de base negativa.

Para que el resultado sea -1/8, hay que elevar 1/2 a -3.

5)

Para realizar este ejercicio he tenido que buscar en bastantes páginas para ver ejemplos, y al final he encontrado una y me he basado en esa para resolverlo.

Por lo tanto, el orden de magnitud sería 10^5885,404 y las cifras del resultado serían o 5885 o 5886.

7)

     Z= 8'68 

     T= 429'9

8)

9)

10)

Por tanto, la cuota de amortización semestral con intereses es de 3400 euros.

Prueba 4

1)



2)

La solución de un sistema de este tipo es un conjunto de números reales que satisfagan simultáneamente todas y cada una de las desigualdades. La solución suele expresarse en forma de intervalo llevando cuidado de expresar correctamente si es abierto o cerrado según el signo de desigualdad utilizado.

3)



4)



7)

Historia de los logaritmos

En análisis matemático, usualmente, el logaritmo de un número real positivo —en una base de logaritmo determinada— es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo en base 10 de 1000 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 10³ = 10×10×10.De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponenciación de la base del logaritmo.Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 3⁵=243 luego log₃243=5. Cuando se sobreentiende la base, se puede omitir.Los logaritmos fueron introducidos por John Napier a principios del siglo XVII como un medio de simplificación de los cálculos. Estos fueron prontamente adoptados por científicos, ingenieros, banqueros y otros para realizar operaciones fácil y rápidamente, usando reglas de cálculo y tablas de logaritmos. Estos dispositivos se basan en el hecho más importante —por identidades logarítmicas— que el logaritmo de un producto es la suma de los logaritmos de los factores:

                                                              

La noción actual de los logaritmos viene de Leonhard Euler, quien conectó estos con la función exponencial en el siglo XVIII.

Pierre de Fermat

Pierre de Fermat (Beaumont-de-Lomagne, Francia; 17 de agosto de 1601​- Castres, Francia; 12 de enero de 1665) fue un jurista y matemático francés denominado por el historiador de matemáticas escocés, Eric Temple Bell, con el apodo de «príncipe de los aficionados».Fermat fue junto con René Descartes y Johannes Kepler uno de los principales matemáticos de la primera mitad del siglo XVII.Joseph-Louis Lagrange afirmó claramente que consideraba a Fermat como el inventor del cálculo. Fermat fue cofundador de la teoría de probabilidades junto a Blaise Pascal e independientemente de Descartes, descubrió el principio fundamental de la geometría analítica. Sin embargo, es más conocido por sus aportaciones a la teoría de números en especial por el conocido como último teorema de Fermat, que preocupó a los matemáticos durante aproximadamente 350 años, hasta que fue demostrado en 1995 por Andrew Wiles ayudado por Richard Taylor sobre la base del Teorema de Shimura-Taniyama.

Hombre erudito y embebido en la cultura clásica grecorromana, era enciclopédico por la amplitud de su bagaje. Hacía anotaciones en los márgenes de los libros que leía, con observaciones y esbozos de demostraciones. No era matemático profesional ni escribía libros. Era de su interés el saber humano de su tiempo. Envía cartas de sus hallazgos o inquietudes, tuvo como mentor y difusor al padre Mersenne, y, en vez de formalizar sus descubrimientos o inventos, posiblemente se dedicaba a especular y daba vuelo a su imaginación desbordante; lanzaba retos mediante problemas cuya solución poseía. Polemizó con Descartes sobre el caso de La Dioptrique obra de este. Ante la incomodidad de Descartes, Fermat envió una prueba, haciendo presente que más le importaba la verdad no la fama ni la envidia.

Sophie Germain

Marie-Sophie Germain (1 de abril de 1776 - 27 de junio de 1831)​ fue una matemática, física y filósofa francesa. Fue una de las pioneras de la teoría de elasticidad​ e hizo importantes contribuciones a la teoría de números; uno de sus trabajos más importantes fue el estudio de los que posteriormente fueron conocidos como números primos de Sophie Germain (números primos cuyo doble incrementado en una unidad es también un número primo).

Germain tuvo un interés especial en las enseñanzas de Joseph-Louis Lagrange y, bajo el pseudónimo de «Sr. Le Blanc», uno de los antiguos estudiantes de Lagrange, le envió varios artículos. Lagrange se impresionó tanto por estos artículos que le pidió a Le Blanc una entrevista y Germain se vio forzada a revelarle su identidad. Aparentemente Lagrange reconoció el talento matemático por encima de los prejuicios y decidió convertirse en su mentor.

Correspondencia con Gauss:

En 1804, después de leer a Carl Friedrich Gauss en su famoso Disquisitiones Aritmeticae (1801), comenzó a cartearse con este, de nuevo bajo pseudónimo.​ Dos años después, durante la invasión napoleónica de Prusia, también Gauss conoció su verdadera identidad, cuando Germain intercedió ante uno de los generales de Napoleón Bonaparte (Pernety), a quien Germain conocía personalmente, para que le resguardara de cualquier daño ante la ocupación de la ciudad natal de Gauss en Brunswick (Braunschweig). Sophie temía que Gauss pudiera correr un destino similar al de Arquímedes y le confió a Pernety sus temores; este localizó al matemático alemán y le dijo quien era su protectora (lo que confundió a Gauss ya que nunca había oído hablar de ella). Entonces Germain le escribió a Gauss una carta en la que admitía su condición femenina; a lo que Gauss contestó lo siguiente:Pero cómo describirte mi admiración y asombro al ver que mi estimado corresponsal, el Sr. Le Blanc, se metamorfosea en este personaje ilustre que me ofrece un ejemplo tan brillante que sería difícil de creer. La afinidad por las ciencias abstractas en general y sobre todo por los misterios de los números es demasiado rara: lo que no me asombra ya que los encantos de esta ciencia sublime solo se revelan a aquellos que tienen el valor de profundizar en ella. Pero cuando una persona del sexo que, según nuestras costumbres y prejuicios, debe encontrar muchísimas más dificultades que los hombres para familiarizarse con estos espinosos estudios, y sin embargo tiene éxito al sortear los obstáculos y penetrar en las zonas más oscuras de ellos, entonces sin duda esa persona debe tener el valor más noble, el talento más extraordinario y un genio superior. De verdad que nada podría probarme de forma tan meridiana y tan poco equívoca que los atractivos de esta ciencia que ha enriquecido mi vida con tantas alegrías no son quimeras, dada la predilección con la que tú has hecho honor a ella.

Sin embargo, en 1808, cuando Gauss fue nombrado profesor de astronomía en la Universidad de Gotinga, el interés del matemático se derivó hacia las matemáticas aplicadas y ambos dejaron de cartearse.

Autoevaluación del primer examen

En primer lugar, cabe destacar, que no estoy nada satisfecho con mi primer examen, por lo tanto voy a ser muy autocrítico. Había ejercicios en el examen que no hice porque no pensé adecuadamente, ya que algún ejercicio era de cursos anteriores, y si llego haber estudiado más, podría haber resuelto alguno más (todos no, era imposible). Creo que sacaré un 3 sobre 22 que estaba puntuado el examen, con esto aprendo que tengo que razonar más los exámenes, y que si tengo que dejar algún ejercicio sin hacer para así poder resolver otros, tengo que hacerlo. Espero que las próximas autoevaluaciones sean mejores, y más positivas.

Resolución del Examen, Ejercicio 7, 8 y 9

Resolución del Examen, Ejercicio 3 y 4

Resolución del Examen, Ejercicio 10

Resolución del Examen, Ejercicio 5

Resolución del Examen, Ejercicio 2

Resolución del examen, Ejercicio 1

a) Un número, en ciencia, es una abstracción que representa una cantidad o una magnitud. En matemáticas un número puede representar una cantidad métrica o más generalmente un elemento de un sistema numérico o un número ordinal que representará una posición dentro de un orden de una serie determinada. Los números complejos se usan como una herramienta útil para resolver problemas algebraicos y que algebraicamente son un mero añadido a los números reales que a su vez ampliaron el concepto de número ordinal. Sobre todo, un número real resuelve el problema de comparación de dos medidas.
0 sí es un número natural, ya que los números naturales van desde el 0 hasta el 9.
El conjunto de números naturales sí que es igual al conjunto de números enteros positivos, ya que son los mismos números (0,1,2,3,4,5,6,7,8,9).
Cualquier número negativo es un número algebraico no radical, ya que no se puede poner un número negativo en forma de raíz.

b)

c) 

Resolución Examen, Ejercicio 6

Preevaluación del examen

La entrada la hago el jueves, ya que el miércoles no tuve tiempo, aun así, pude anotar en una hoja los primeros pensamientos tras acabar el examen. Vayamos por partes; en primer lugar cabe destacar que el examen era muy difícil completarlo en menos de 1 hora, ya que eran 10 ejercicios y en ninguno se tardaba poco; en segundo lugar, la dificultad del examen era elevada, mi compañero y yo no fuimos capaces ni de plantear todos los ejercicios, ni mucho menos resolverlos. Según salí del examen me fui decepcionado, ya que había estudiado bastante las semanas anteriores, y en el examen entre nervios y tiempo, no pude concentrarme y hacer el examen dando lo mejor de mí. Me costó mucho hacer los ejercicios de la primera cara del examen, pues aunque se resolvían de una manera similar a la de clase, los enunciados eran un poco difíciles, y en algún caso liosos. Además hubo ejercicios como el número 10, que tan siquiera sabía por dónde empezar, leía el enunciado y no sabía a que se refería. El ejercicio que se resolvía por el método de Gauss, se me dio bien, a pesar de que muchas gente dijo que era incompatible, o que les daba soluciones "raras", yo pude resolverlo siguiendo un procedimiento similar al de clase, pero con pequeñas variaciones para así no liarme. En resumen, salí bastante disgustado del examen, y sin muchas esperanzas de aprobar esa prueba, ahora me dispongo ha resolver en casa tranquilamente el examen, ver los fallos, los ejercicios que no supe hacer y corregir así mis fallos para una próxima ocasión.

Víspera del Examen

Estoy escribiendo en esta entrada a las 12 y 40 de la noche, pues se me había olvidado este ejercicio, pero gracias a Twitter y al último Twit que ha publicado nuestro profesor, seré capaz de realizar esta tarea previa al examen. Entrando en materia, sobre el examen de matemáticas, lo veo con miedo, ya que el profesor nos ha dicho que podremos llevar el libro y los apuntes al examen, lo cual quiere decir que va a ser un examen bastante complicado, a parte de largo, que ya nos lo avisó.

Voy más o menos preparado, ya que llevamos repasando el examen varias semanas, haciendo ejercicios en clase, y resolviendo dudas. El día previo al examen, Martes 4 de Diciembre, estuvimos repasando 3 ejercicios que se resolvían mediante el método de Gauss, posiblemente nos encontremos un ejercicio similar a los que estuvimos practicando.

De este examen, a parte de una calificación sobre 10, espero llevarme la nueva experiencia de realizar un examen con un compañero, y las actividades que nos ha propuesto el profesor después de realizar el examen (autoevaluación, preevaluación y corrección del examen). Según nuestro profesor, es más importante el trabajo diario a lo largo de este primer trimestre, que la nota del examen de clase, con lo cual, nos ha dicho que no vayamos preocupados y con nervios a dicha prueba.

Mañana realizo el examen, ya os comentaré en futuras entradas como me ha ido, y las conjeturas y observaciones que saco, con esto me despido, y desearme suerte.

Diofanto de Alejandría

Diofanto de Alejandría nacido alrededor del 200/214 d. C. y fallecido alrededor de 284/298 d. C., fue un antiguo matemático griego. Es considerado "el padre del álgebra maestral".Nacido en la raja, de él nada se conoce con seguridad sobre su vida, salvo su edad con la que falleciera; esto, gracias al epitafio redactado en forma de problema y conservado en la antología griega.

Transeúnte, esta es la tumba de Diofanto: los números pueden mostrar, ¡oh maravilla! la duración de su vida. Su niñez ocupó la sexta parte de su vida; después, durante la doceava parte, de vello se cubrieron sus mejillas. Pasó aún una séptima parte de su vida antes de tomar esposa y, cinco años después, tuvo un precioso niño que, una vez alcanzada la mitad de la edad de su padre, pereció de una muerte desgraciada. Su padre tuvo que sobrevivirle, llorándole, durante cuatro años. De todo esto se deduce su edad.

 donde la incógnita ${\displaystyle x}$ representa la edad que le cupo vivir a Diofanto.

Según esto, Diofanto falleció a la edad de 84 años. Se ignora, sin embargo, en qué siglo vivió. Si fuera el mismo astrónomo Diofanto que comentó Hipatia (fallecida en 415), habría fallecido antes del siglo V; pero si se tratase de personas distintas, cabe conjeturar que habría vivido a finales de dicho siglo, ya que ni Proclo ni Papo lo citan, lo que resulta difícil de entender tratándose de un matemático que pasa por ser el inventor occidental del álgebra. En opinión de Albufaraga, Diofanto vivía en los tiempos del emperador Juliano, hacia 365, fecha que aceptan los historiadores. Según otra fuente habría vivido en el siglo III de nuestra era .

Gerolamo Cardano

Gerolamo Cardano fue un médico, además de un matemático italiano del Renacimiento, astrólogo y un estudioso del azar. Este filósofo y enciclopedista fue autor de una de las primeras autobiografías modernas. También es conocido por ser el primero en publicar una solución general completa de la ecuación de tercer grado y de la ecuación de cuarto grado, y por sus aportaciones a la mecánica, como la suspensión cardán que lleva su nombre.

Algunas de sus publicaciones matemáticas son:

• Practica arithmetice et mensurandi singularis, Milán, 1539 
• Artis magnae, sive de regulis algebraicis —conocido como Ars Magna—, Núremberg, 1545. 
• Opus novum de proportionibus numerorum, motuum, ponderum, sonorum, aliarumque rerum mensurandarum. Item de alia regula, Basilea, 1570. 
• Liber de ludo aleae.

Carl Friedrich Gauss

Carl Friedrich Gauss fue un matemático, astrónomo, geobotánico y físico alemán que contribuyó significativamente en muchos campos, incluida la teoría de números, el análisis matemático, la geometría diferencial, la estadística, el álgebra, la geodesia, el magnetismo y la óptica.​ Gauss ha tenido una influencia notable en muchos campos de la matemática y de la ciencia, y es considerado uno de los matemáticos que más influencia ha tenido en la historia. Fue de los primeros en extender el concepto de divisibilidad a otros conjuntos.

Gauss pronto fue reconocido como un niño prodigio, pese a provenir de una familia campesina de padres analfabetos; de él existen muchas anécdotas acerca de su asombrosa precocidad. Hizo sus primeros grandes descubrimientos mientras era apenas un adolescente en el bachillerato y completó su magnum opus, Disquisitiones arithmeticae, a los veintiún años (1798), aunque fue publicado en 1801. Fue un trabajo fundamental para que se consolidara la teoría de los números y ha moldeado esta área hasta los días presentes.